宇宙に知的生命は存在するのか?そしてもし存在するとすれば、それはどれほど一般的なのか?あるいは、地球外知的生命体探査(SETI)に携わる人々がいつかそれに遭遇する可能性はどれくらいなのか?数十年にわたり、科学者たちはこのトピックについて激しく議論してきた。この主題に関して書かれた多くの論文や研究から、主に2つの陣営が浮かび上がってきた:私たちの銀河に生命は一般的だと信じる人々(いわゆるSETI楽観主義者)と、地球外知的生命体はまれであるか存在しないと主張する人々(SETI悲観主義者)である。
最近の論文で、David Kipping教授(「Cool Worlds」の本人)とGeraint Lewisは、この議論をより詳しく検討し、Jaynesの実験として知られる確率分析の形式に基づいて新しい見解を提示した。この方法を天体生物学とドレイクの方程式に適用することで、彼らは私たちの銀河における知的生命の存在が「すべてか無か」の命題である可能性があると結論付けた。故Arthur C. Clarke(偉大な科学者かつSF作家)の言葉を引用すると:「2つの可能性が存在する:私たちは宇宙で孤独か、そうでないかのどちらかだ。どちらも等しく恐ろしい」。
David Kippingはコロンビア大学の准教授で、ハーバード大学天文台のCarl Sagan Fellowである。彼はまた、コロンビア大学のCool Worlds Labの主任研究者でもあり、この研究室は系外惑星系の研究と特性評価に専念している。Geraint Lewisはシドニー大学物理学部のシドニー天文学研究所の天体物理学教授である。彼らの論文「Do SETI Optimists Have a Fine-Tuning Problem?」は最近オンラインで公開され、International Journal of Astrobiologyでの出版に向けて審査中である。
ドレイクの方程式
1961年、著名な天文学者Frank Drakeは、ウェストバージニア州のGreenbank天文台で初めてのSETI会議を主催した。この会議の準備として、彼はSETI研究者が直面する課題を要約した方程式を作成した。これはドレイクの方程式(Drake equation)として知られるようになり、数学的に次のように表される:
N = R* × fp × ne × fl × fi × fc × L
ここで:
- N は現在活動中で通信可能な文明の数(銀河系内)
- R* は銀河系内での恒星形成率
- fp は惑星を持つ恒星の割合
- ne は惑星を持つ恒星1つあたりの、生命を潜在的に宿すことができる惑星の数
- fl は上記のうち、実際に何らかの生命が発生する割合
- fi は上記のうち、知的生命が発生する割合
- fc は上記のうち、星間通信能力を発展させる割合
- L はそのような通信可能な文明が活動している期間
を表す
ドレイクの方程式は銀河系内の地球外文明(ETC)の数を推定することを意図したものではなく、SETIについての対話を促進するためのものだった。Drakeが最初に定式化して以来、この方程式は批判、追加、改訂の対象となり、その過程でしばしば誤って解釈されてきた。Kipping教授がUniverse Todayへの電子メールで説明したように、問題の一部はパラメータに値がしばしば恣意的に適用されることだ:
「ほとんどのパラメータを知らないので、これは純粋な推測であり、そのように表示されるべきです。もう一つよく見落とされる点は、これが文明の平均数を表しており、したがって、何らかの基礎となる分布の期待値であるということです。最近では、Drake方程式を批判することが一種のスポーツになっています。確かに、それを計算機として使用する人は正当に批判されるべきですが、基本的な考え方は間違っていません。そこには何らかの数の文明が存在するはずで、原則として、関連するパラメータを収集してそれを計算することができます。問題は正確な定式化、どのパラメータを含めるべきか、それらが本当に何を意味するのか、そして時間変動性のようなニュアンスをどう扱うかにあります」。
Jaynesの実験
Edwin Jaynes(1922-1998)はワシントン大学セントルイス校のWayman Crow特別物理学教授だった。1968年、彼は実験室の人が未知で表示のない化合物(化学物質X)の入った瓶を提示される実験を想像した。実験台に沿って、水で満たされた多くのビーカーがあり、実験はその中で化学物質Xがどれくらいの頻度で溶解するかをテストするものだった。Jaynesは、化合物がほぼすべての場合で溶解するか、ほとんど溶解しないかのどちらかを予想すべきだと主張した。
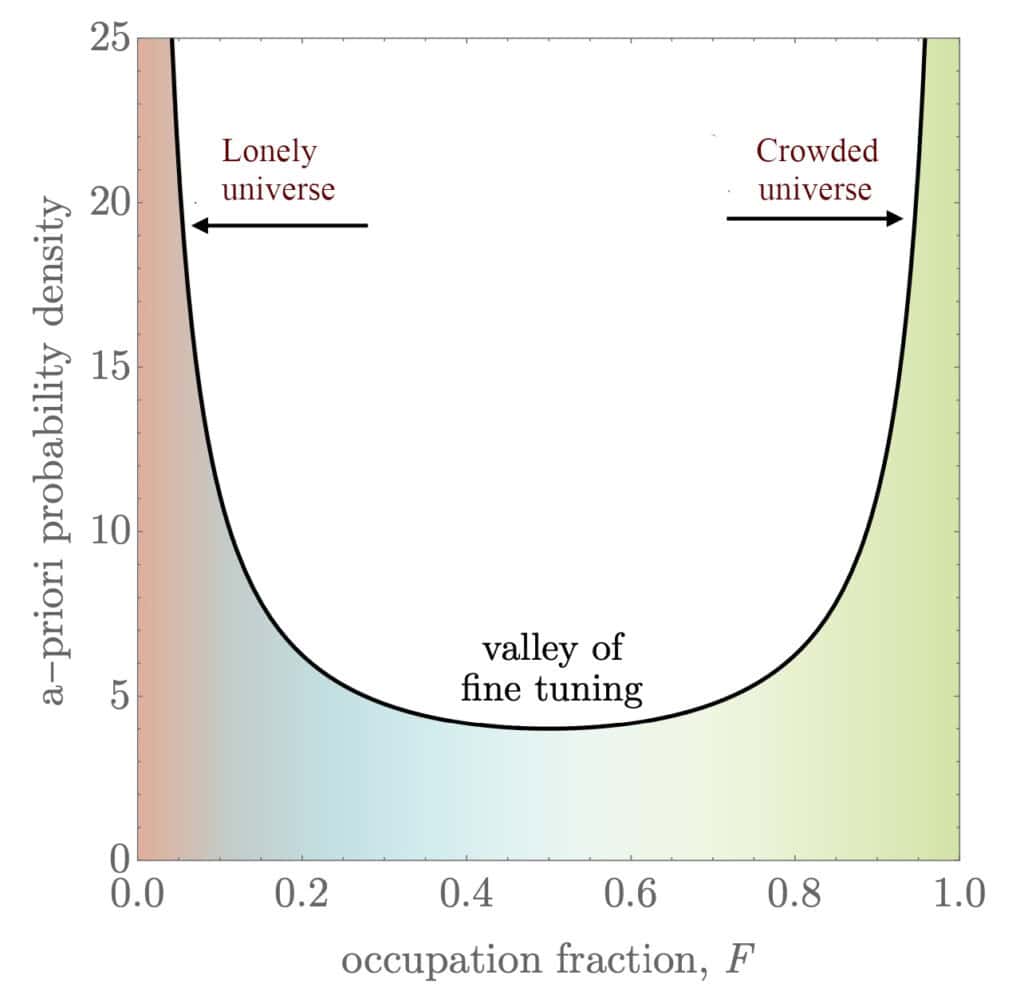
グラフにプロットすると、確率分布はボウル型になり、0と1でピークを示す。Kippingはさらに詳しく説明した:
「Jaynesは一連のベルヌーイ実験を想像しました。つまり、はい/いいえの答えを返す実験です。これは実際には何でもよいのですが、例として、彼は未知の化学物質を水の入った一連のビーカーに溶かし、そしてそのうちどれくらいの割合が溶けるかを尋ねることを想像しました。別の科学者、伝説的なJohn Haldaneは、すでに約50%という答えはア・プリオリにありそうもないと示唆していました。ほとんどすべてが溶けるか、ほとんど溶けないかのどちらかを期待すべきだと。
Jaynesはそれを厳密に証明し、客観的ベイズ推論の多くのツールを開拓しました。我々は同様に、考慮中のベルヌーイ実験を他の質問に置き換えることができます。例えば、どれくらいの割合の恒星がブラックホールになるかなど。観測を得る前に、約50%という答えは驚くべきものでしょう。これは恒星質量の分布が、臨界質量閾値の上下でちょうど半分ずつになるように微調整されていることを意味します。実際には答えは1000分の1で、これはJaynesの立場に沿っています」。
統計学分野への多大な貢献により、Jaynesは「客観的ベイズ主義」の創始者の一人とされている。彼の実験はそのようには意図されていなかったが、KippingとLewisはその天体生物学への潜在的な応用を見出した。
すべてか無か?
1983年の画期的な論文「The Great Silence – the Controversy Concerning Extraterrestrial Intelligent Life」で、David Brinは地球外生命の存在に関する継続的な議論に取り組んだ。これから、彼は議論に関して2つの陣営の存在を見出した:「接触楽観主義者」と「接触悲観主義者」 – あるいはKippingとLewisが論文で言及するところの「SETI楽観主義者」と「SETI悲観主義者」 – 人類が接触できる文明が銀河系に存在すると信じる人々と、人類が宇宙で孤独であるため無意味だと信じる人々である。
Jaynesの実験を銀河系における知的生命の問題に適用すると、それが非常に一般的であるか、非常にまれであるかのどちらかを期待すべきである。確率分布が最も弱い中間(つまり、地球外生命が半ば一般的)では、「微調整問題」が浮上する。宇宙論と天体生物学の文脈では、微調整とは、生命の条件が特定の普遍的定数が非常に狭い値の範囲内にある場合にのみ発生し得るという提案を指す。
これらの基本的な定数のいずれかがわずかでも異なれば、宇宙は物質、大規模構造、または我々が知っているような生命の発展に適さないものになるだろう。Kippingが説明したように、これはSETI楽観主義者にとって問題を提示する:
「先ほど挙げたブラックホールの例とは異なり、この問題には下限がありません。ブラックホールの場合、天体物理学から最小と最大の許容される恒星質量がわかっており、それはわずか数桁の範囲です。ブラックホールの閾値はその比較的狭い範囲のどこかにあるはずです。宇宙人に関しては、知性の確率は1%か0.000….00001%(好きなだけゼロを追加できます)かもしれません。
そのような広大な可能性の範囲があるため、SETI楽観主義者は、その%値が誰かをまだ見ていないほど高くはないが、確実に妥当な低確率の深淵よりもはるかに高いという、かなり不自然な見方を信じなければなりません。つまり、本質的に微調整問題があり、その割合がかなり狭い範囲内に収まる必要があるのです」。
もし私たちの銀河が地球外文明で満ちているならば、確かに我々が気付くはずの否定できない兆候があるはずだ – つまり、電波信号、巨大構造物、クラーク・バンド、その他の「テクノシグネチャー」である。これが馴染みのある話に聞こえるとしたら、それはフェルミのパラドックス(我々が一連の記事を書いたもの!)の核心そのものだからだ。そのため、KippingとLewisの議論はSETI悲観主義の一例と解釈することができる。幸いなことに、話はここで終わらない。
新しい形式主義
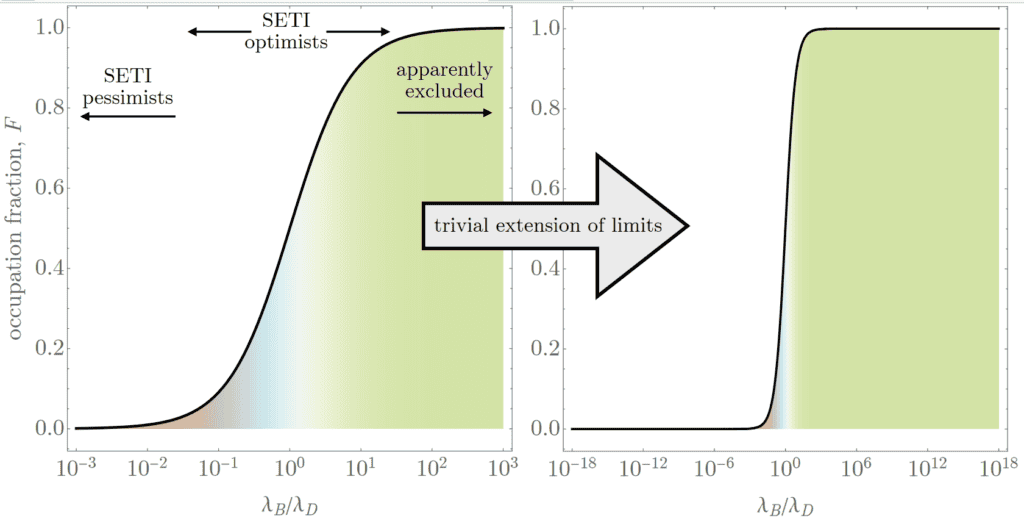
この結果に直面して、KippingとLewisは、文明の誕生率と死亡率という2つのプロセスのみを考慮したDrake方程式の新しい形式主義を考案しようとした。これを行うと、方程式のすべてのパラメータ(文明の寿命Lを除く)が単一のパラメータ:文明の誕生率と死亡率(rc)に収束する。つまり、数学的には次のように表される:NC = rc x LC。Kippingは述べた:
「標準的なドレイクの方程式では、どのパラメータを含めるべきかについて議論に巻き込まれがちです(例えば、生命が多細胞生命に発展する確率の分数があるべきか、など)。しかし、すべての文明には必ず始まりと終わりがあることは完全に否定できません。実際、この枠組みでは望むなら死亡率をゼロに設定することもでき、これは無限の寿命に対応します。生態系、例えばペトリ皿のような系では、明確に定義された最大可能人口があり、これを収容力と呼びます。そこで、我々はこのニュアンスを考慮に入れるために、誕生-死亡バージョンのDrake方程式を更新しました」。
この場合、確率分布はS字型になったが(上の画像参照)、最終的な結果は同じだった:銀河は混雑しているか、空っぽかのどちらかである。これを回避する一つの方法は、人類がETCが出現し、銀河全体に拡大し始めている期間に生きており、したがってまだ我々の機器で気付かれていないという考えだ。しかし、KippingとLewisが示したように、これも微調整問題に苦しむ。なぜなら、生物学は人口成長が加速する現象であることを示しているからだ。
「ご覧のように、銀河規模の拡大段階は宇宙的な時間尺度では比較的速いはずです。実際、まさに瞬きのような速さです」とKippingは言う。「そのため、そのような段階に生きている可能性は低いのです。あなたがより生きている可能性が高いのは、これが起こる前の本質的に空の銀河か、それが起こった後(実際、これは議論の余地がありますが、あなたの惑星が植民地化されているため不可能です)です。」再びフェルミのパラドックスが頭をもたげ、最も強い可能性は、人類が孤独であるか、パーティーに早く到着したか、現在天の川銀河に存在する少数の文明の一つであるかのいずれかだということになる。
SETIへの希望?
しかし、すべてが悪いニュースだと思う前に、KippingとLewis は、SETIは専用のリソースを提供するに値する重要かつ不可欠な実験であることを強調している。 「成功する確率は低いように見えるが、そのような成功は間違いなく人類史上最もインパクトのある科学的発見となるだろう」と彼らは結論づけている。 また、Hansonの「Grabby Aliens」仮説(人類はS字カーブの中間点におり、数億年以内にETIに遭遇する)等、希望を持ち続ける理由をいくつか提示している。 その一方で、キッピングはSETIがより広い網を張ることで利益を得られる可能性も示唆している。 もし彼らの研究が示唆するように、我々の銀河系に高度な文明が存在するのが非常に稀である(あるいは存在しない)なら、銀河系外に目を向けるべきである。 「私の好きな考え方は、我々の銀河系が異常に静かなだけで、ほとんどは忙しく満ちあふれている。 「これはありえないことのように思えるが、おそらく、居住可能な領域がすでに食い尽くされているため、賑やかな銀河系で生まれることは不可能なのだろう。 このことは、我々が銀河系外SETIにもっと重点を置くべきことを示唆している」。
論文










コメント