地球が太陽の周りをどのように公転しているか教わったことがある人なら、私たちの惑星は楕円形の軌道を描いており、1年のある時期は他の時期よりもずっと太陽に近づいていると思うかもしれない。ほとんどの教科書がそう示しているからだ。
実際、多くの人が地球は冬よりも夏の方が太陽に近いと思い込んでいる。偶然にも、これは南半球の夏には当てはまるが、北半球の夏には当てはまらない。
南半球では、地球は冬よりも夏の方が太陽に500万km近いが、北半球ではその逆だ。地球と太陽の平均距離は1億5千万キロで、季節がある主な理由は、地球が傾いているため、それぞれの極が太陽の方を向いているときもあれば、太陽から遠ざかっているときもあるからだ。
そのため、地球の軌道は完全な円軌道から比較的わずかなずれしかない。しかし、なぜ地球の軌道は卵型に見えるのだろうか?また、どのようにすれば実際の状況を視覚化できるのだろうか?
自転車の車輪を考えてみよう
地球の公転軌道がどれほど円形なのか、また他の惑星がどれほど円形なのかを理解するために、私は地球の公転軌道の形を26インチの自転車の車輪と比較してみることにした。実際のホイールの偏差が何を意味するかについて調べて欲しいその結果、私はとても驚いた。

軌道は以前考えていたよりもはるかに真円に近かったのだ。もしこの軌道が26インチ(660.4mm)の自転車のホイールだとしたら、真円からのずれは0.1mm以下だろう。肉眼では真円と見分けがつかない。
他の惑星も見てみた。金星と海王星の軌道はさらに真円に近く、金星の軌道はわずか14μm(μmは100万分の1メートル)、海王星は31μmしかずれていない。
最も円軌道の少ない惑星は火星と水星である。火星の軌道を26インチの自転車の車輪に見立てると、わずか3ミリ弱のズレになる。
水星の軌道は最も真円度が低く、14mmずれているが、それでもわずか2%である。
もしあなたが自転車を持っているなら、その車輪は火星の軌道ほど真円ではない可能性がある。縁石や岩にまともにぶつかったことがあるなら、前輪は水星の軌道よりも円形でないかもしれない。
わずかなズレ
もし地球が太陽から平均1億5,000万キロメートル離れていて、その距離が1年間で500万キロメートル変化するのだとしたら、その軌道のずれは3%強になるはずではないか?
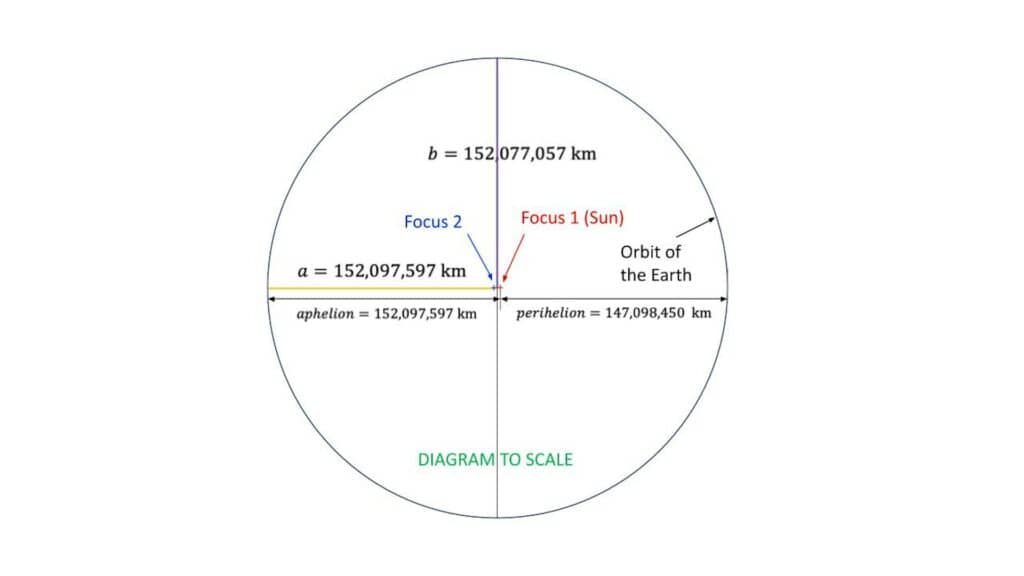
この質問に対する答えは、太陽は楕円の中心ではなく、焦点と呼ばれる点として片側にオフセットされている。もし惑星が形成される際に、重力に対抗するためにちょうど良い速度で移動すれば、それは円を描いて移動することになる。
しかし、現実の宇宙では、惑星がちょうど円を描くような速度で移動することはほとんどない。楕円軌道でなければ達成できない。
一周する
数千年前、古代ギリシャ人は、すべての天体は地球の周りを公転し、完全な円を描いて移動すると信じていた。
ポーランドの天文学者Nicolaus Copernicus(1473~1543年)が、惑星(地球を含む)が実際に太陽の周りを公転していることに気づくまで、この考え方は約1,500年間支持された。
Copernicusはその軌道が円形だと考えた。その後、ドイツの天文学者であり数学者でもあったJohannes Kepler(1571-1630)が、自分の考えが間違っていることに気づき、惑星運動の3つの法則を考え出した。
最初の法則は、惑星の軌道は楕円であり、円ではないというものだ。第3の法則は、惑星の軌道の大きさとそれにかかる時間を結びつけるもので、ここではちょっと複雑すぎて説明できない。
第二の法則は、太陽から任意の惑星まで線を引くと、惑星が移動するにつれて、その線は等しい面積を等しい時間で掃き出すというものだ。ピザを思い浮かべてほしい。大きなピザの幅の狭い部分は、小さなピザの幅の広い部分と同じ面積を持つことができる。これは、惑星が太陽に近いほど速く動くからである。
教科書で軌道が楕円で描かれる主な理由は、ケプラーの第二法則を実証するためである。もし地球の軌道が正しく縮尺された図のように描かれていたら、くさびの違いを見ることはできないだろう。
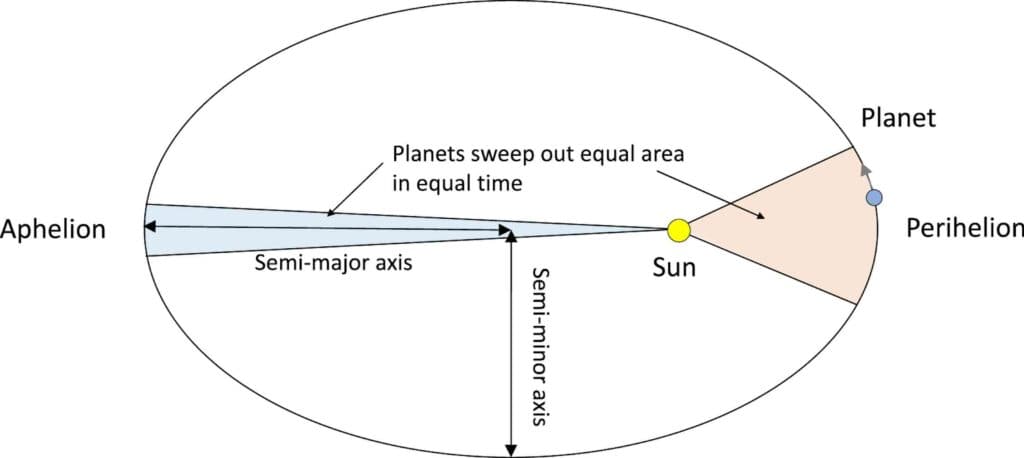
しかし、これでは地球の軌道が実際よりもはるかに楕円であるかのような印象を与えかねない。これは誇張であり、重要な特徴を強調した一種の数学的戯画である。
古代ギリシャ人は、地球が太陽系の中心にあることについては間違っていたが、惑星の軌道については大きく間違っていなかった。というわけで、ダジャレを許してもらえるなら、私たちは一周したのである。









コメント